3.2 计算机科学中的模型

图灵和冯诺依曼模型

从算盘到计算机，人类走过了漫长的历史。计算机发展的转折点往往都是一些大师提出关键模型的时期，了解这些模型可以帮我们更好理解计算机世界。

计算机是数学的延伸和应用，图灵机模型是一个分水岭，图灵机和可计算性理论让自动计算具有了理论基础。虽然在此之前的模型也很重要，但是还停留在数学上，比如数理逻辑中最重要的一部分——布尔代数。

新一代的软件工程师已经不再关注计算机是如何工作的了，他们把计算机当做一种可以通过编程语言对话的"生物"来看待了。我曾被问到过，我们日常使用的"电脑"为何被称作计算机，它和计算看似毫无关系。

要回答这个问题需要将图灵和冯诺依曼模型两个计算机科学基础模型清晰地分开。

计算机能够发展出这么多的功能，其实这只是一个偶然，现代计算机的各种高级应用是计算机的研究者们没有想到的。布鲁斯·斯特林创作了一本小说，名字叫做《差分机》。这本小说是为了致敬查尔斯•巴贝奇，巴贝奇设计了一种机械计算机，这种计算机需要通过蒸汽驱动，这就是差分机。在某个平行宇宙中，人类走向了由差分机带动的新一轮技术革命，不过这种技术革命还是蒸汽时代的延续。

理论上讲，全自动的机械计算机是能够被制造出来的，因为"程序"在图灵模型中被表述为"有限执行的操作序列"，所以很多东西都可以看做计算机。

算盘会被经常和计算机一起提到，算盘是人力驱动的一种计算机，算珠的状态可以看做寄存器。对中国人来说理解图灵机非常简单，我们可以使用算盘来类比。当算盘归零后，算盘的状态为初始状态，每一次拨动算珠就是一个指令，当所有的指令下发完成，算盘上最终状态就是计算结果。指令序列就是算法，算盘就是一个状态机。

在算盘之后的时代，还有计算尺，甚至手摇计算机。手摇式计算机算一种半自动的计算机，我国科研人员曾使用它进行原子弹的计算工作。

计算机带有计算两个词的功劳得归到图灵。图灵在 1937 发表了论文阐述可计算性这个概念，并给出了计算机的抽象模型。图灵在论文《论可计算数及其在判定问题中的应用》中，提出了著名的理论计算机的抽象模型——"图灵机"。

它描述了这样一种机器：一个虚拟的机器，由一条无线长的纸带和读写头组成。纸带上分布有连续的格子，并能被移动，读写。机器能读取一个指令序列，指令能对格子纸带进行移动和读写。和算盘的逻辑一样，机器每执行一个指令，纸带的状态就发生了变化，最终完成计算。

在电子计算机中，图灵模型是由门电路完成的，门电路就是开关电路。记录状态的门电路可以想象为算盘上算珠的拨动位置。门电路有开关两种状态，因此能通过简单的方法实现加法器，进而实现各种运算。

通过开关就能做出计算机？听起来在开玩笑，用机械来实现当然无比复杂，但是用电气来实现就非常简单。所有的运算都可以通过加法完成，这个不难理解。加法如果用电器开关来表达，只需要做到下面几种条件：

• 0 + 0 = 0 0 + 0 = 0

• 1 + 0 和 0 + 1 = 1 1 + 0 和 0 + 1 = 1

• 1 + 1 = 10 1 + 1 = 10

如果把每个数字想象为两个灯泡的话，怎么设计一个电路满足上面三种情况让相应的灯泡亮起、熄灭。因此要通过电气实现图灵模型就需要实现指令的基本元素：加法器，以及一个存储结构：锁存器。

理解原始计算机的基本原理只需要理解加法器和锁存器是如何制作出来的，这个不是玄学，只需要初中物理学就能搞定，可以参考书籍《编码——隐匿在计算机软硬件背后的语言》，这本书讲述了计算机从简单的电气结构到复杂结构的完整演化过程。

图灵模型只是描述了如何一步一步的完成计算任务，这种机器称不上"电脑"。让一堆"沙子"具备通灵般能力的人是冯·诺依曼。现代的计算机实际上是一个死循环，可以类比为冲程发动机，才让计算机看起来有了生命。

ENIAC 是公认第一个满足图灵模型的电子计算机，ENIAC 通过纸带编写程序，并拨动开关执行和获得结果。冯诺依曼在比 ENIAC 更先进的计算机项目 EDVAC 中描述了另外一种模型，他认为程序本质上也是一种数据，将指令和数据共同存放到内存中，这些指令中存在特殊的跳转指令，让程序周而复始的运行。

存储程序模型构建了一个能自我运行的计算模型，构成了一个系统。处理器和内存之间使用总线连接，用来给这个系统提供输入的设备叫做外设，每一次指令循环可以访问一次外设传入的信号，这就是中断。

想象一台由继电器组成的计算机，如果每一次执行指令计算机会发出 "嘚" 的声音，图灵模型就是程序开始运行后线性的 "嘚嘚嘚……嘚嘚停"。冯·诺依曼的模型就是上电后 "嘚嘚嘚嘚嘚……中断……嘚嘚嘚嘚嘚"，并反复循环。冯·诺依曼让计算机永不停息，并产生交互效果。

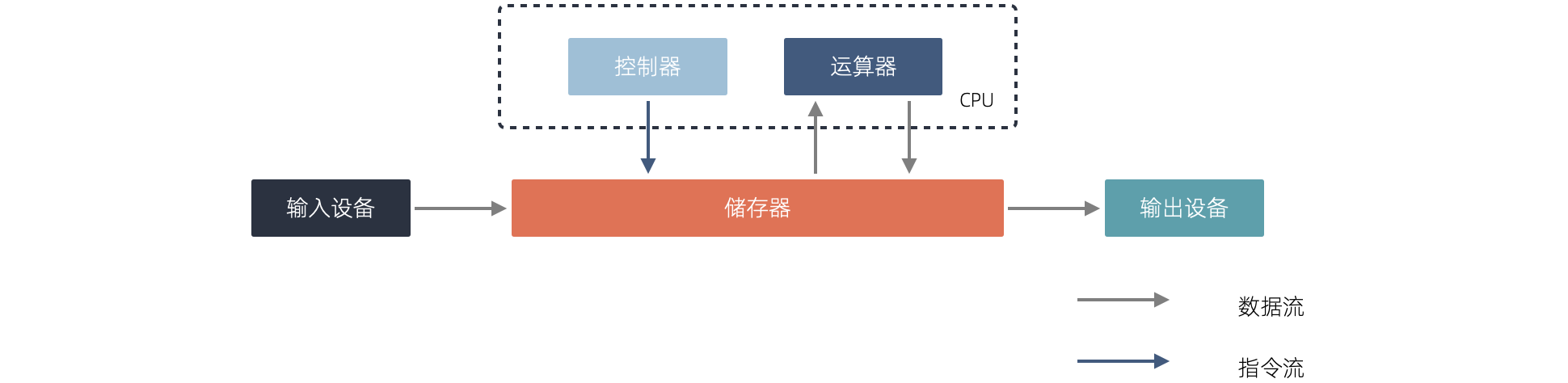
我将计算机科学基础模型展开，每种模型都能作为计算机科学的原料：

• 布尔数学逻辑模型：为开关电路组成复杂的逻辑规则提供了数学工具。 布尔数学逻辑模型：为开关电路组成复杂的逻辑规则提供了数学工具。

• 加法器的电气模型：实现全加器，为图灵模型提供基础指令。 加法器的电气模型：实现全加器，为图灵模型提供基础指令。

• 图灵模型：算法是有序的操作序列，数据是状态，计算的过程就是有序修改状态。 图灵模型：算法是有序的操作序列，数据是状态，计算的过程就是有序修改状态。

• 冯·诺依曼模型：算法也是数据，算法可以控制指令序列的跳转，然后无限循环下去，进而可以响应外部的信号输入。 冯·诺依曼模型：算法也是数据，算法可以控制指令序列的跳转，然后无限循环下去，进而可以响应外部的信号输入。

在我朴素的认知里：冲程发动机、计算机、生命是一类事物，启动后便不再停下，直到能量耗尽或受到外界的干预。

自动推理模型（理解编程语言）

各种各样的编程语言层出不穷，由于工作的需要会接触不同的编程语言。如何能理解编程语言的本质是什么呢？我尝试找一些模型简化对编程语言的理解。先用矛盾论分析一下编程语言解决的是什么矛盾：

所以人类设计出来各种各样符合人类习惯（各不相同）的方式编写程序，这些编写程序的模型就是高级语言。要使用自己定义的语法规则来写程序，就需要一个转换器，能将符合人类习惯的语法进行转换，这就是编译器。

一门新的语言需要满足几个条件：

• 新定义的语法必须是形式化的。 新定义的语法必须是形式化的。

• 新定义的语法能方便的被转换。 新定义的语法能方便的被转换。

• 人们能接受这种语法编写程序。 人们能接受这种语法编写程序。

所以编译器是一个自动推理机，只要能被推理的形式化语言都可以作为输入。除了自然语言无法实现之外，无论用中文、表情包、符号、图形都能作为一种编程语言的形式。

编译的过程有：语法分析、词法分析、语义分析、中间代码和优化、目标代码。大师通过编译过程学习如何实现编译器，普通工程师可以反过来用这个过程理解一门新的语言。

我尝试为编译过程中的环节找到一个现实中的类比来理解编译器，将其类比为人类阅读法律文书（法律文件是最贴近形式化的自然文本）。

词法分析

扫描，识别代码 Token，将关键字、变量、操作符提取出来

处理调查材料，案件人员、行为等要素

语法解析

将 Token 组织为一棵树(AST) 用于推理

将人员和行为映射成图谱，形式逻辑推理

语义分析

处理上下文相关的信息

识别行为发生的动机、背景，提取上下文信息

中间代码

上面三步是前端，中间代码是为了多平台代码生成用

整理为卷宗

目标代码

根据不同的平台进行代码生成

输出到报纸、网站等媒体

尝试找到一些通俗的模型理解编译过程，在 https://craftinginterpreters.com/a-map-of-the-territory.html 这个网站下介绍了一个清晰的编译过程。

理解编译器后再学编程语言就清晰很多，比如语法（Grammar）有三个层次：

• 词法（Lexical）：决定哪些表达式、关键字是否合法。 词法（Lexical）：决定哪些表达式、关键字是否合法。

• 句法（Syntax）：决定一个句子是否合法，比如流程语句。 句法（Syntax）：决定一个句子是否合法，比如流程语句。

• 语义（Grammar）：决定一段代码的组织结构是否合法，函数、类、闭包等规则。 语义（Grammar）：决定一段代码的组织结构是否合法，函数、类、闭包等规则。

Lexical 和 Syntax 往往可以看成一体，Grammar 不太一样，在一些编译器中 Syntax 和 Grammar 的错误提示都不太一样。所以可以这样看一门语言：Syntax 是类 C 的还是非类 C 的，Grammar 上是面向对象的还是面向过程的，是否支持闭包这类上下文追溯的能力。

理解推理模型可以用来帮助学习编程语言，比如 TypeScript 可以编译成 JavaScript，很多时候我们不需要特别学习 TypeScript，将小段 TypeScript 代码编译一下，看看生成的 JavaScript 是什么就行了。